Expanding Fractions

The opposite of simplifying fractions is "complicating" or expanding fractions. :-)

And although it may seem that simplifying is more common, expanding is needed very often.

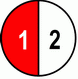
We can’t compare fractions with different denominators – so we usually expand fractions to make their denominators alike.

Same goes for adding and subtracting fractions – we can’t do a thing unless the denominators are alike – so again – expanding.

Concerning fraction to decimal conversion, if it’s convenient to expand the fraction to get 10ths (or 100ths or 1000ths etc) in the denominator – conversion becomes piece of cake. More about this in its appropriate section.

Expanding fractions is usually used when we are:

• Comparing fractions
• Adding fractions
• Subtracting fractions
• Fraction to decimal Conversion

Numerator being only the quantity, is not as important as denominator. So whatever we do from the above stated – we focus on the denominator.

Let’s see some examples:

If I have only 1 half of pizza left, and I want to split it with you, after the split we’ll still have one half but cut into half, i.e. 2 fourths.

	1	×2	=		2
	2	×2			4

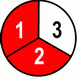
And if two more friends arrive and we cut those pizza quarters to half – we get 4 eights – but the original "amount" of pizza still remains the same – one half.

	2	×2	=		4
	4	×2			8

Those fractions that have the same value are called equivalent fractions. So when we are reducing or expanding fractions we are operating with equivalent fractions.

With fractions this is a two-way street. While we can’t "sew up" pizza slices – with fractions you can – and "sewing up pizza slices" is called simplifying or reducing fractions.

Let’s see another example:

We have thirds here, and let’s say that for some reason we need 12ths. So what are we going to do? We multiply our fraction by 4/4 (we’re actually multiplying by 1) – and we get our 12ths.

	2	×4	=		8
	3	×4			12

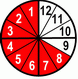
As we can see – the red area doesn’t change, only the number of pizza slices.

Of course, the same analogy goes for every other case, even the complicated ones.

For instance we have 8ths and need 64ths.

So, from the fact that 8 x 8 = 64, we’ll expand our fraction by 8/8 – and voila, we have our 64ths.