Comparing Fractions

I guess you already know we're not comparing fractions on a hunch. ;-)

So, we need to be aware of certain things before we start:

• What happens with a fraction when we're changing the denominator
  (if a numerator stays the same)?
• What happens with a fraction when we're changing the numerator
  (if a denominator stays the same)?
• Which fraction is bigger?
  (different denominators and numerators)

Let’s look at all these cases. First two cases are just warm ups, and the third is about comparing fractions.

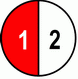
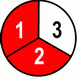
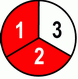
Reminder: Red pizza slices are leftovers and more red is bigger! :-)

First we'll look into:

What happens with a fraction when we're changing the denominator?

• Numerator = 1
• Denominator - increasing
• Fraction - decreasing

	1		>		1		>		1		>		1
	2				3				4				5

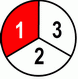
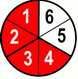
Obviously where there is more red pizza leftover – that’s bigger.

Our conclusion is: bigger denominator => smaller fraction.

If previous example wasn’t enough for you, here’s a similar example with numerator being 2.

• Numerator = 2
• Denominator - increasing
• Fraction - decreasing

	2		>		2		>		2		>		2
	1				2				3				4

But again, we draw the same conclusion – with our denominator growing bigger => our fraction is getting smaller.

---

Second we'll look into:

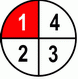
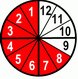
What happens with a fraction when we're changing the numerator?

• Numerator - increasing
• Denominator = 1
• Fraction - increasing

	1		>		2		>		3		>		4
	1				1				1				1

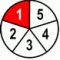
Aha, now is the opposite. We see that by increasing our numerator we make our fraction bigger.

And again for the sake of me being smart again, let’s see another example but this time with our denominator being 2.

• Numerator - increasing
• Denominator = 2
• Fraction - increasing

	1		>		2		>		3		>		4
	2				2				2				2

Yup, the same story. If our numerator "grows" => the whole fraction "grows" too.

---

And now finally:

Which fraction is bigger?
(different denominators and numerators)

Let’s look at this example and try to conclude what sign should we put between these two fractions:

	3		?		4
	4				6

I guess it’s obvious now when we see the pizzas, but without it we won’t be able always to see the difference so clearly.

So we're going to expand these fractions to make their denominators alike, and then we’ll just compare the numerators.

In our case the LCD for 4 and 6 is 12. So in order to get 12ths we’re going to multiply or expand the first fraction by 3/3, and the second one by 2/2.

	3	×3	?		4	×2
	4	×3			6	×2

So, now we have this:

	9		>		8
	12				12

Aaaa, now the numbers clearly confirm what we’ve already concluded from the pizza images - that the first fraction is bigger by 1/12.

Apart from expanding, sometimes simplifying fractions can be a more reasonable step.

You'll see what I mean in this next example.

	8	÷4	?		10	÷5
	12	÷4			15	÷5

We simplified the first fraction with 4/4 and the second one with 5/5 and got:

	2		=		2
	3				3

They are the same. Again, maybe the pizzas helped seeing this in the first place, but simplifying really helped seeing it clearly.

On the other hand, if we would have expanded the fractions (LCD for 12 and 15 is 60), we would have got the same result, but as you can see - this was a much more elegant solution.

Let’s try another example, but now without the pizzas.

4	?	5
5		6

Aaaah, what now? :-)

Well, don’t worry, we follow the previous pattern. First we expand our fractions to get the same denominators. LCD for 5 and 6 is 5 × 6 = 30. So we expand or multiply our fist fraction by 6/6 and the second one by 5/5.

4	×6	?	5	×5
5	×6		6	×5

Our new situation shows that it was a tight race. Horse number 25 won by a smidgen! ;-)

24	<	25
30		30

Before we wrap up this comparing fractions page, I want to draw your attention to something very important:

Don't mix up a numerator with a denominator!

Here, the following might help:

	4		>		3
	3				4

Well, that about all you need to know about comparing fractions. Anyway, let's summerize it below.

Conclusion for comparing fractions section: Of the two fractions with like numerators – the bigger is one with the lower denominator. Of the two fractions with like denominators – the bigger is one with the bigger numerator. Of the two fractions with different denominators and numerators, after we expand or simplify fractions to make their denominators alike, the one with a bigger numerator is the winner.

---

Go from Comparing Fractions to Math Help With Fractions Go from Comparing Fractions to Free Math Help Online - Home Page