Help With Decimals

Loading

To digress a little: similar is with percents. They are even more specific fractions. They are fractions stuck with a 100 as their denominator.

Pi (not pie) is a very famous decimal number. Let me show you on it the general idea about decimal place values.

Decimal noting is actually very useful as it simplifies a much more robust number notation. Let me show you on Pi.



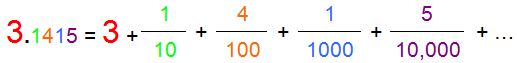
You must agree that what’s on the left hand side of equal sign is much simpler than all that forest of fractions on the right.

---

Now let’s see another example again with 1 decimal place.

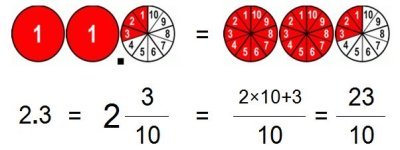
A point (dot) is a separation point between whole numbers part on the left, and the fractions part (respectively 10ths, 100ths, 1000ths etc) on the right hand side.

This example, 2 wholes and 3/10, is represented by 2.3. We notice that there are no 10ths stated anywhere. That’s because they are already implied.

If you're interested in more of this examples - go to decimal to fraction conversion page.

---

Comparing Decimals

Now let’s see how to compare decimal numbers.

We have to be aware that decimals are a combination of whole numbers and 10 based fractions. We also know that the bigger parts are always on the left hand side.

So in order to compare two decimal numbers, first we should compare the whole-number parts (the most left part) and if they are the same – we move on to comparing the decimal-number parts, i.e. 10ths, and if those parts are the same – we move one to 100ths, etc.

So in order to compare two decimal numbers, first we should compare the whole-number parts (the most left part) and if they are the same – we move on to comparing the decimal-number parts, i.e. 10ths, and if those parts are the same – we move one to 100ths, etc.

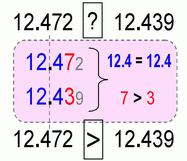
Example # 1.

-  3 > 2,

-  3 (wholes) is more than 2 (wholes),

-  therefore the following 10ths on the right doesn’t matter

-  3.4 > 2.6

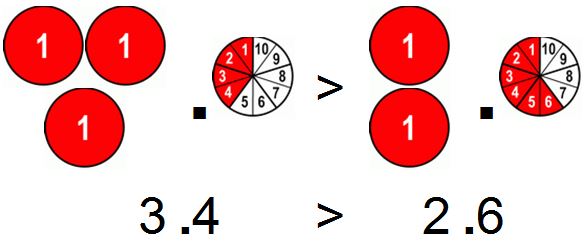
NOTE: As general rule of thumb – you align the dots and compare from left to right.

---

Example # 2.

Now if this was the case:

-          1 = 1,

-           we have the same number of  whole numbers on both sides,

-          so we expand our comparing to 10ths

-          3/10hs < 7/10ths, so

-          our right number is the winner

---

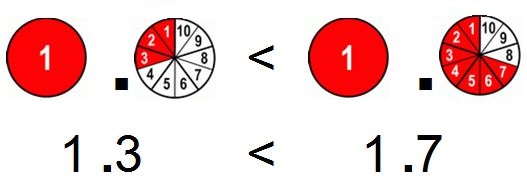
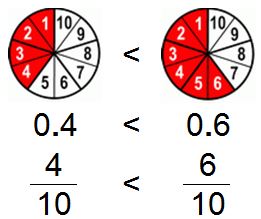
Example # 3.

Here’s another similar example:

-          0 = 0

-          4 < 6 (all 10ths)

-          0.4 < 0.6

---

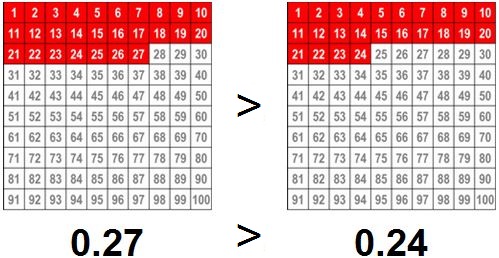
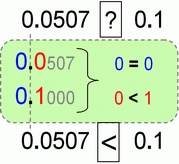
Example # 4.

-          0 = 0,

-           we have the same number of  whole numbers on both sides,

-          so we expand our comparing to 10ths

-          2 = 2 (all 10ths)

-          Now we expand our comparison to 100ths

-          7 > 4 (all 100ths), so

-           0.27 > 0.24

---

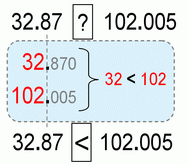
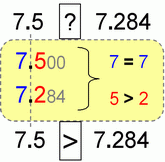
And a few more quick examples (maybe I over did it, but it’s better to be safe than sorry):

IMHO, it is best if you vertically align the numbers by decimal point. Then it’s clearer what you’re dealing with. As always we go from left to right.

---

Adding Decimals

Adding decimals is pretty much the same as adding whole numbers.

The best strategy is to align all the numbers vertically by its decimal point (i.e. putting all decimal points of all decimal numbers exactly below one another), and then just add vertically as usual (with carrying as necessary).

We do this because we want to add whole numbers with whole numbers, and 10ths with 10ths, 100ths with 100ths etc, and the vertical placement makes it easier for the eye.

After that you can even pretend like there is no decimal point at all.

So again there’s not much to say here if you know you way around with adding whole numbers.

Here are some basic examples. I’ll try to follow up with some worksheets soon.

To make things more obvious, there are no whole numbers in the following addends. I’ve made it as a little animation:

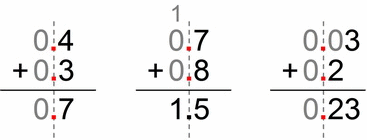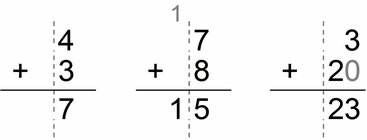
It’s even easier when we put the whole numbers part. Again if we imagine we’re dealing with whole numbers, it would be something like this (stare at the image below ;-)):

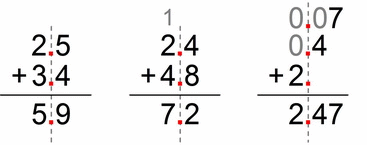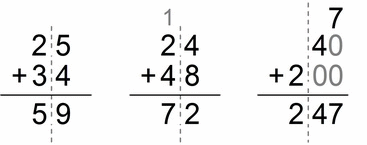
So, very similar, don’t you think?

If you really need additional help adding with this, I suggest you to visit my “vertical addition” page.

---

Subtracting Decimals

As with addition, there is not much to add other than it is almost the same as the classic subtraction. If you know your way around with regular vertical subtraction then this will be easy for you.

So, you align all decimal numbers vertically by its decimal point (dot), and then subtract as usual (with borrowing if necessary). After the above mentioned alignment you can act like there is no decimal point.

Ok, enough of this tail chase, let’s see some examples.
I won’t go into negative numbers yet, so these are only positive results.

First let’s start with no regrouping (borrowing):

Example # 1:

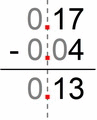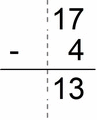
These animated images are showing you that when you align the decimals by a decimal point, you can subtract the decimal numbers like regular whole numbers temporarily ignoring the zeros:

-          it’s like we have multiplied by 100 (that means we moved the decimal point two places to the right):

-          17 – 4 = 13

-          and then after getting our result we again divide by 100 (that means moving a decimal point back to its old place – two positions to the left):

-          13 / 100 = 0.13

 

---

Example # 2:

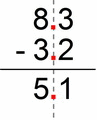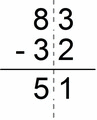
Same thing here, you remove the decimal points and voila – you have a regular 2 digit vertical subtraction :

-          to get the whole numbers in this case we multiply by 10 (moving our decimal point only one place to the left => where it becomes “invisible” ;-) )

-          83 – 32 = 51

-          so again we reverse the action by dividing by 10:

-          51 / 10 = 5.1

---

Ok, 2 more examples of subtracting decimals without regrouping:

Example # 3:

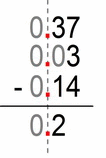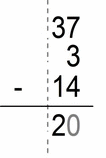
Now a more complicated example, but a same story. Remove the zeros and a decimal point and subtract. At the end you put them back in.

-          0.37 × 100 = 37

-          0.02 × 100 = 2

-          0.14 × 100 = 14

-          we must transform (multiply) all the “actors” with the same “decimal-point-remover”.

-          37 – 14 – 3 = 20

-          and to get back to previous state:

-          20 / 100 = 0.2

 

---

Example # 4:

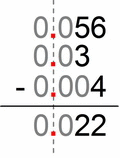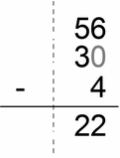
Don’t let the zeros scare you. Align the dots, remove zeros and do a classic subtraction kicks in.

-          56 – 30 – 4 = 22

-          0.056 – 0.03 – 0.004 = 0.022

 

We can see how it seems much harder when the numbers are not vertically aligned by dot. One can easily make a mistake and be confused. So, my advice to you is – always subtract decimals vertically.

 

---

Now let’s see some examples of subtracting decimals with regrouping (borrowing):

Example # 5:

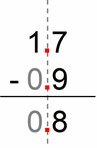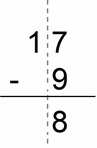
-          we multiply all numbers by 10 to get rid of decimals (moving the decimal point 1 place left)

-          then we “break” 9 to 7+2 (we subtract to 10, and then from 10, check out “number breaking”), i.e.

-          17 – 9 = 17  –  7–2 = 10 – 2 = 8

-          8/10 = 0.8

 

---

Example # 6:

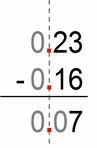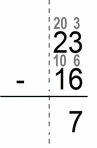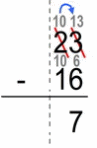
-          we multiply by 100 (to move the decimal point to places to the right)

-          23 – 16

-          then we “borrow” the 10 from first number (minuend)

-          23 – 16 = 10+13 – 10-6 = 10-10 + 13 – 6 = 7

-          at the end we divide by 100 to get back to where we started

-          7/100 = 0.07

---

Ok, 2 more examples of subtracting decimals with regrouping:

Example # 7:

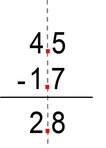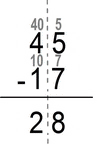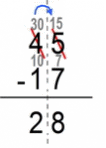
-          we multiply by 10, and get:

-          45 – 17 (whole numbers)

-          usually we subtract units from units and 10s from 10s, but now our minuend unit 5 is less than subtrahend 7, so we borrow a 10 from 45 (minuend) to reinforce the 5 into 15

-          30+15  -  10-7 = 30-10  +  15-7 = 20+8 = 28

-          we reverse by dividing by 10

-          28/10 = 2.8

 

---

Example # 8:

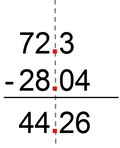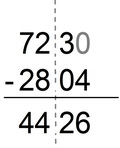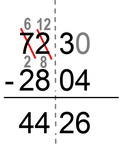
-          we multiply by 100 (because the 2 subtrahends have 100s), so

-          7230 – 2804

-          we can divide this subtraction into 2 parts:

-          7230 – 2804

-          we can completely separate this example because 30 is greater then 4, therefore there is no need for borrowing 10s from the blue part;

-          we can easily subtract the red part:

-          30-4 = 26

-          now, we’re stuck with the blue part:

-          72-28

-          again, usually we subtract units from units, and 10s from 10s (and 100s from 100s etc), but in this case minuend unit 2 is less than subtrahend 8, and we “call the backup” and borrow a 10 from 70:

-          60+12  -  20-8 = 60-20  +  12-8

-          40+4 = 44

-          so our result is 4426

-          rolling back by dividing the result by 100 (thus moving the decimal point back to places to the left)

-          4426/100 = 44.26

 

I guess I’ve complicated this enough. :-)

---

Well, I'm back. It's been a while since I've built a page. I hope you like this little help with decimals page.

Return from Help With Decimals to Free Math Help Online - Home Page