Fraction to Decimal
Conversion

Before we dig into fraction to decimal conversion, you should be familiar with some fraction 101 like expanding and simplifying fractions , what are the numerator and denominator etc. But most of all I recommend you to look at decimal to fraction conversion. It’s much easier and it’s the opposite of what we’re trying to do here. So examine the vice versa in order to deepen the understanding of converting fractions to decimals.

Here's what you can find on this page: 3 types of division Special conversion cases Regular conversion cases

Well, fraction to decimal conversion is actually classic division (we could say, for later grades). It’s doing division all the way.

So let’s say something more about division itself, because this story is all about division.

---

You should know that we have:

3 Types of Division

• Division without remainder: quotient is a whole number

		=
6	= 6÷2	=	3
2

Q = 3

This is classic no remainder, clean and "most wanted" division. ;-)

• Division with remainder: quotient is a whole number, plus we have another "indivisible" whole number as a remainder on the side.

		=		+
7	= 7÷2	=	3	+		1
2						2

Q = 3   R = 1

We can't divide number 1 by 2 and get a whole number as a result, so we leave it indivisible as 1/2. Number 1 is in this case our remainder. This type of division is actually an intro to:

• "Full" division (divides even the remainder part): quotient is a decimal number.

This means, it consists of a whole number part, and a decimal (fraction) part.

		=		.
7	= 7÷2	=	3	.	5
2

Q = 3.5

Why the ".5" part instead of the 1/2? Because we must present our decimal part within a based-on-10s fraction system. So, we expanded 1/2 to get 10ths:

			=
	1		=		5
	2				10

So, in this case we’ve managed to represent our remainder in 10ths, but if we couldn’t, we would’ve gone further and tried representing it in 100ths, 1000ths, 10,000ths etc, by dividing further.

In our case of fraction to decimal conversion we’re dealing with this final type – getting decimal numbers out of fractions.

---

There are some:

Special cases of
Fraction to Decimal Conversion

that can be solved really quickly, and the rest is just plain old division till you die. ;-)

Let’s start with easy classic examples, and then build our way up.

The simplest conversions from fraction to decimal is when we have 10ths, 100ths, 1000ths etc, as a denominator. So let’s give those examples first.

The following principle applies: How many zeros = that many decimal places.

In the following example we have only one zero in the denominator, that means that we’re going to have only one decimal place at the end of our conversion.

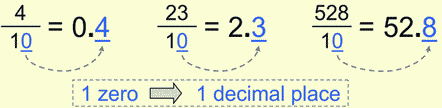
There is another angle that you can look at this. If we imagine there is an “invisible” decimal point right next to the numerator number (like 4. and 23. and 528.), we can see that it has “emerged” after dividing by 10 and moved to the left for 1 decimal space.

Digression: When we divide by 10s decimal point goes to the left, and when we multiply by 10s – it goes to the right.

We have the same analogy in our next example. Now we have two zeros in the denominator, which means that we’re going to have two decimal places "after" the decimal point.

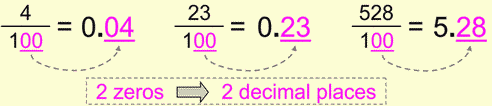
Or looking at it from the above mentioned second angle, our "invisible" decimal point has "resurfaced" and, because of two zeros in the denominator, has moved two decimal places to the left.

Finally let’s see "three-zeros" example, just to make sure we’re on the same track here. So now we have 3 zeros in the denominator – hence the 3 decimal places in the decimal number.

As you can see if we don’t have "enough" numbers to put in, and we must honor the "same-number-of zeros-and-decimal-places" rule => we input zeros. :-)

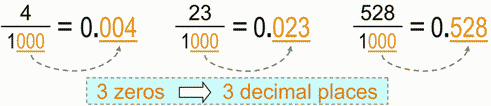
And the second approach: our former invisible decimal points, due to 3 zeros in the denominator, have "reappeared" and "traveled" 3 decimal places to the left.

These were the easiest examples. Let’s see some slightly harder examples. Those would be where we can expand or simplify our fractions to get 10ths, 100ths, 1000ths etc for our denominator, because afterwards the previous rule applies.

Whenever the opportunity arises, we should avoid division. That’s usually doable when we have the following numbers as denominators:

5 and 2 can be used to get 10ths (because of 5×2 = 10) 4, 5, 20, 25 and 50 can be used to get 100ths (because of 2×50 = 4×25 = 5×20 = 100)

So in order to get 10ths, 100ths, 1000ths etc, we can:

• expand
• simplify, or
• combine the above two

Look at the following example.

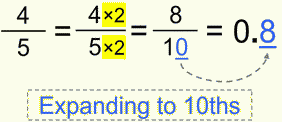
As you remember, expanding is multiplying both a numerator and a denominator by a same number. And since our goal is to get 10ths, we multiplied 5ths by 2, and afterwards it’s easy-peasy.

Of course, same applies for the halves:

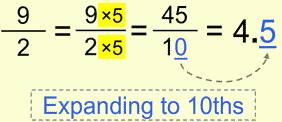
Well, as we mentioned earlier, there may be cases when is much more convenient to simplify to get 10ths, rather than to expand.

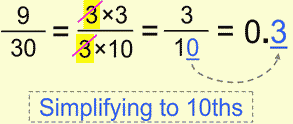
This works of course because we conveniently had the common factors up and down.

Now if you’re really determined to avoid plain old division – you can try combining those two.

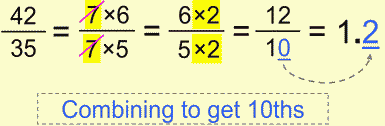
As you can see, we combined simplifying and expanding in order to get 10ths. Sometimes this won’t be so obvious but it’s worth trying if it doesn’t take much of your time.

Here’s another combination.

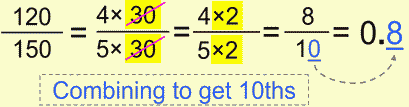
I guess you’re wondering: "When the heck are we going to see the real fraction to decimal conversion here?!" Easy tiger, we’re getting there. :-P

This is a necessary process, trust me. Sometimes slower is faster (or something like that). Understanding is knowing.

Now let me show you some 100ths tricks.

This is expanding to 100ths:

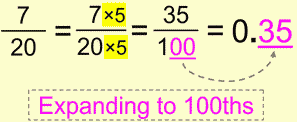
And of course we’re expanding because we can’t simplify to 10ths, because 7/2 won’t give us a whole number. So we’re multiplying by 5, and applying the same principle as before (number of zeros in the denominator = number of decimal places after the decimal point).

Here’s an example of simplifying to 100ths:

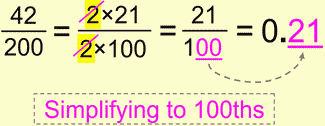
I guess this was really obvious, but it’s here to illustrate a point that you can use it and save yourself from division if you can recognize it.

Let’s wrap this simplifying/expanding stuff with its combo.

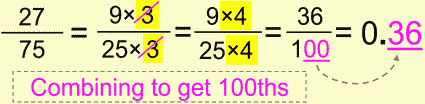
This one was maybe a stretch, but it still depicts what can be done if you practice a little. Believe me, math is all about recognizing patterns, and for that you need practice.

---

Finally I think it’s time to do some:

Regular
Fraction to Decimal Conversion

No special cases, no bending your gray cells, just plain old division.

But before we move on, you should know this: 5 = 5 = 50 = 500 = 5000 =... 1 10 100 1000 This, of course applies for every number. You get the picture...

Again, to illustrate a point, let’s start with easy examples.

Fraction to decimal conversion, one-decimal-place case.

We see that number 2 goes 1 time into 3 (1×2 = 2 < 3), which leaves us with the remaining 1. We turn that 1 into tenths (10/10) and divide again by 2. Only this time we have to place the resulting 10ths in its appropriate place value – at the first decimal place after the decimal point.

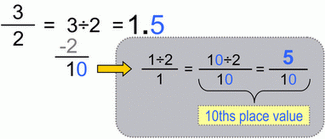
Fraction to decimal conversion, 2-decimal-places case.

Number 4 goes 2 times into number 11 (2×4 = 8 < 11), which leaves us with the remaining 3. As before, we turn that 3 into tenths (30/10) and divide by 4 again. We see that 4 goes 7 times into 30 (4×7 = 28 < 30), which leaves us with remaining 2/10. Then we represent those 2 tenths as 20/100 and divide it by 4. We can see that 4 goes 5 times into 20, which leaves us with no remainder and our job is done. Of course, those 5/100 are noted in its appropriate decimal place value.

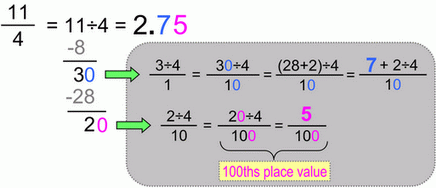
Fraction to decimal conversion, 3-decimal-places case:

We see that 8 goes 3 times into 25 (8×3 = 24 < 25), remainder is 1. That 1 becomes 10/10, we divide again by 8. 8 goes 1 time into 10, remainder is 2 (actually 2/10). We turn that 2/10 into 20/100 and divide again by 8. 8 goes 2 times into 20, remainder is 4 (actually 4/100). We turn those 4/100 into 40/1000 and divide again by 8. 8 goes 5 times into 40, no remainder – job well done. :-) And again, those 10ths, 100ths and 1000ths must respetively go to its right decimal place value spot.

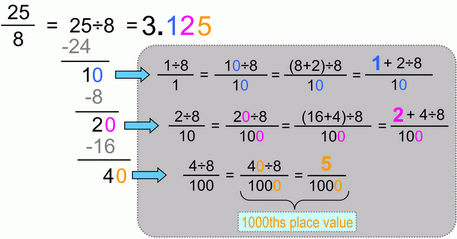
Much has been said on this page, and I guess most of the fraction to decimal conversion ground is covered. If you are really, and I mean really crazy about this topic – drop me a line and I’ll elaborate more. :-)

---

Go from Fraction to Decimal Conversion to Math Help With Fractions Go from Fraction to Decimal Conversion to Free Math Help Online - Home Page