Adding Fractions

How to add fractions you wonder?

Well, hear this - we can’t do a thing unless we have like denominators.

If you’re wondering what’s a denominator, then check out our math help with fractions page for more basic info about fractions.

If we’re having 2 or more fractions with like denominators – adding them is easy – we add their numerators and that’s it. No heavy science there, just plain old addition.

But if that’s not the case, we have to expand or simplify fractions to make them alike, i.e. we must find their LCD (least common denominator), and afterwards add their numerators.

So, let’s progress through the following cases:

Adding fractions with like denominators:

numerators = 1, like denominators
numerators > 1, like denominators

Adding fractions with unlike denominators:

Adding Fractions
With Like Denominators

As I said earlier, this is really easy. With like denominators, we add the numerators, carry the denominator and that’s it. I think that the best way to show this is through examples.

We'll be separating the following examples in two parts.

First we’re dealing with the most simple version with numerator being one, and denominator being the same.
Then we’re going to use numerators greater than 1, keeping the denominators alike, of course.

First case of
Adding Fractions with Like Denominators

Numerators = 1
Like Denominators


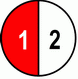
1	+	1	=	1+1	=	2	=	1	= 1
2	+	2	=	2	=	2	=	1	= 1

As you can see – we had two halves, so it’s even visually obvious that we’re going to get 1 whole (number) once we add them (or "sew" them up).

Now what about this one:


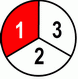
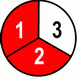
1	+	1	=	1+1	=	2
3	+	3	=	3	=	3

Even by saying what we see on the left hand side: two thirds – we got the answer. :-)


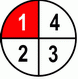
1	+	1	=	1+1	=	2	÷2	=	1
4	+	4	=	4	=	4	÷2	=	2

This one has little simplifying at the end. Two fourths = one half.

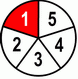
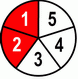
Now let’s finally look at fifths and sixths.


1	+	1	=	1+1	=	2
5	+	5	=	5	=	5

Same story here, adding numerators…


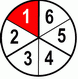
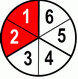
1	+	1	=	1+1	=	2	÷2	=	1
6	+	6	=	6	=	6	÷2	=	3

Again a little reducing of fractions from sixths to thirds.

As you can see, this is as easy as it gets fraction-wise. You can’t get any simpler than that.

Now let’s complicate things just a little bit. We are keeping the same denominator, but changing the numerator.

Second case of
Adding Fractions with Like Denominators

Numerators > 1
Like Denominators


3	+	2	=	3+2	=	5	=	2	1
2	+	2	=	2	=	2	=	2	2

As you can see we have an option to write down our solution as 5/2, which is an improper fraction format, or we can write down 2 and 1/2 which is a mixed fraction format (see types of fractions for more info).

Now let’s try some thirds.


2	+	4	=	2+4	=	6	÷3	=	2
3	+	3	=	3	=	3	÷3	=	2

In this case we can simplify our solution from 6/3 (improper fraction) to 2 wholes (meaning 2 whole numbers).

Now let's see some 4ths.


3	+	2	=	3+2	=	5	=	1	1
4	+	4	=	4	=	4	=	1	4

I guess you’re starting to see a pattern here – with our denominators being alike, we add the numerators, see if our sum "crossed over" for 1 or more whole numbers, plus the proper fraction "leftovers" (in this case 1/4) – and that’s it.


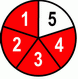
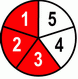
4	+	8	=	4+8	=	12	=	2	2
5	+	5	=	5	=	5	=	2	5

These were the fifths, now let’s finish with sixths.


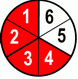
7	+	4	=	7+4	=	11	=	1	5
6	+	6	=	6	=	6	=	1	6

This visual combination of fractions represented by pizza pies and numbers should be very useful. You can keep picturing this "duality" even when we remove the pizzas from the picture. It is important that you don’t mix up a numerator with a denominator.

Continue to Adding fractions with unlike denominators.