Multiplying and Dividing Decimals

This is a second part of help with decimals. In this section we’re explaining multiplying and dividing of decimals.

From the table of content below you can jump to any topic concerning decimals.

Table of content for help with decimals:

And something extra:

Let's start this second part with:

Multiplying Decimals

Multiplying decimals is very much like multiplying whole numbers. The only nuisance is where to put a decimal point. But once you get it – that’s not a problem. So, give me 10 minutes of your time please. :-)

Like always, I’ll go through examples.

Let’s consider these combinations:

Decimal (< 1) × a whole number
Decimal (> 1) × a whole number
Decimal × 10s, 100s, 1000s…
Decimal × decimal
Some pointers for decimal multiplication

1. Decimal (<1) × whole number:

Let us take a very simple decimal number 0.1

Pay attention to the animated image below:

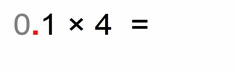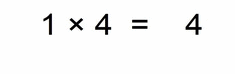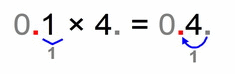
- first we multiply the non-zero numbers part 1 × 4 = 4

- then we count the total number of decimal places of both factors – in this case we have only 1 (0.1 has only one decimal after the decimal point, and 4 has none)

- then we move the decimal point of our solution (number 4) from a far right position to left for 1 place, and we get: 0.4

- (this was actually dividing a 4 by 10)

Let's see another example:

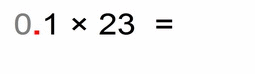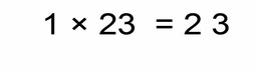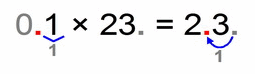
Same story here (this may be an unnecessary example):

- first we multiply the numbers 1 × 23 = 23

- then we count the total number of decimal places of both factors – in this case we have only 1 (again 0.1 has only one decimal after the decimal point, and 23 has none)

- then we move the decimal point of our solution (number 23) from a far right position to left for 1 place, and we get: 2.3

Now let’s try with some other decimals. First the one with 2 decimal places.

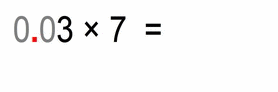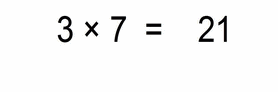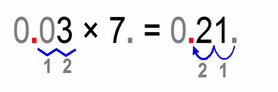
Similar story:

- first we multiply the numbers 3 × 7 = 21

- then we count the total number of decimal places of both factors – in this case we have 2 (0.03 has two decimals after the decimal point, and 7 has none)

- then we move the decimal point of our solution (number 21) from a far right position to left for 2 places, and we get: 0.21

- (this was actually dividing by 100 and multiplying by 3)

Now the one with 3 decimal places (they don’t all have to be zeros, but I’m complicating things gradually)

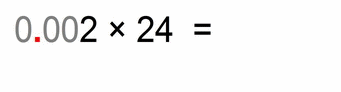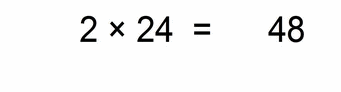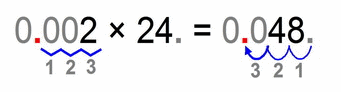
- we multiply the numbers 2 × 24 = 48

- then we count the total number of decimal places of both factors – in this case we have 3 (0.002 has three decimals after the decimal point, and 24 has none)

- then we move the decimal point of our solution (number 48) from a far right position to left for 3 places, and we get: 0.048

- (this was actually dividing by 1000 and multiplying by 2)

Now let’s see another segment:

2. Decimal (>1) × whole number:

This is very similar to previous, so we'll consider 4 examples together.

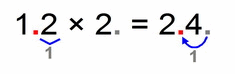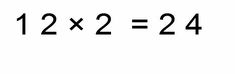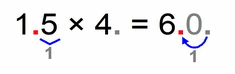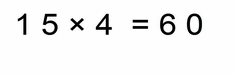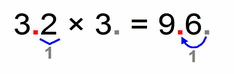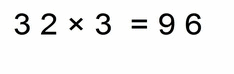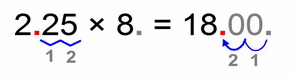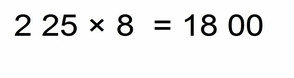Let’s run over those next few examples:

- we ignore the decimal point for the moment

- we multiply the numbers:

- 12 × 2 = 24

- 15 × 4 = 60

- 32 × 3 =96

- 225 × 8 = 1800

- if our factors have one, two (or more) decimal places:

- our solution will have one, two (or more) decimal places

It doesn’t matter if some of our factors are two digit numbers, we count only the decimal places since their number is relevant to the number of decimal places for our solution:

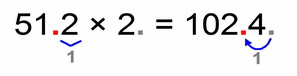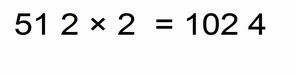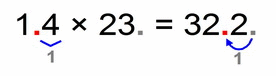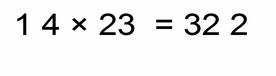3. Decimal number ×10s, 100s, 1000s…

Pay attention, this is very useful and you should often use this trick.

If we want we can move the decimal points of our factors when we multiply. The important thing is to move them in opposite directions. So for example, if we move the decimal point of one factor for two decimal places to the left, we have to move the decimal point of other factor two decimal places to the right.

Example 1:

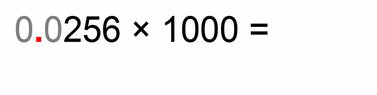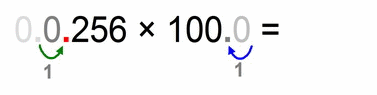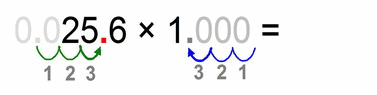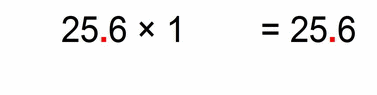
In the above case we had to move the decimal points 3 decimal places. After moving, we regularly multiply. The whole point of this decimal-places-moving is to simplify the multiplication to make it easier for the eye and mind.

So:

- we “move” our (far right therefore invisible) decimal point of our “1000” for 3 decimal places to the left, and we get (number): “1”

- therefore we HAVE to move the decimal point in “0.0256” for EXACTLY 3 decimal places in the opposite direction (to the right), and we get: “25.6”

- at the end we simply multiply our “transformed” factors: 25.6 × 1 = 25.6

Example 2:

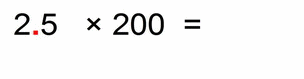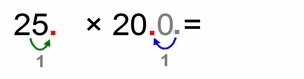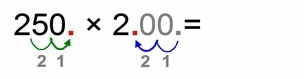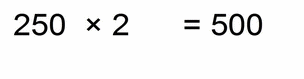
In this case we have one step more to go.

- we “rob” our hidden decimal point at the end of “200” for two decimal places to the left to get number “2”

- then we “boost up the strength” of our “2.5” with those two new decimal places to the right, and we get “250”

- after this “hand-over transfer” we have: 250 × 2 = 500

4. Decimal × decimal:

Finally we’ve come to this most common case. The previous three cases were only preparing us for this. Let’s start with the examples for a change ;-)

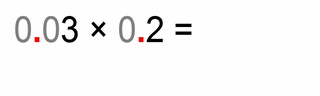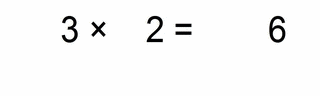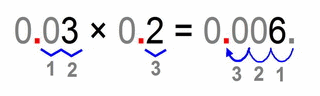
This is a very simple example but it represents the essence of decimal multiplication. It shows you the steps that are the same for all other more complicated cases.

As you can see from the animation:

- we multiply the “non-zero” parts: 3 × 2 = 6

- then we count the total number of decimal places (all places on the right hand side of the decimal point): 0.03 has two, and 0.2 has one, altogether that’s three decimal places in our solution

- that means that we have to move the decimal point of our solution 3 places to the right (all round numbers have their invisible decimal point on the far right bottom corner)

- our final solution is: 0.006 (totally three decimal places)

Now some quick examples. Take a good look at each one of them:

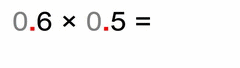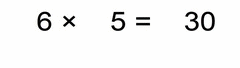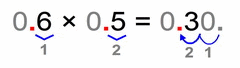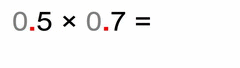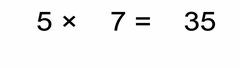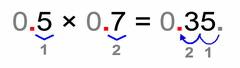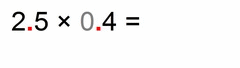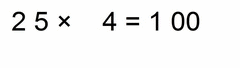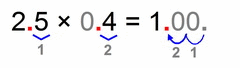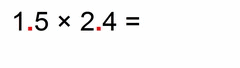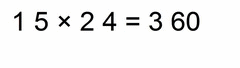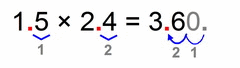Same analogy as in the example (0.03 × 0.2) above these four:

- we multiply the non-zero parts

- count the total number of decimal places in our factors (same goes if there are more than two factors)

- our solution must have that many decimal places (as all factors together)

- (if there’s a zero on the far right, it will eventually become invisible)

5. Some good pointer for decimal multiplication:

At the end, let me give you a few pointers, so that you could feel free to transform decimal numbers to your pleasing:

The first pointer: In this example we can see that we can move the decimal points of our factors in opposite directions and nothing happens to our solution.

So, we can transform our multiplication any way we like.

The second pointer: the number of decimal places must stay the same on both sides of the equation!

If we have 10s or 100s etc in one of our factors (i.e. zeros to the far right of our numbers) – those count as “negative decimals” (I’ve totally coined this expression off the cuff just now :-) ) and we subtract them from the “real-decimals” in other factors.

I believe I’ve made myself perfectly obscure. But luckily, you’ll get from the animated image below.

That’s it. That’s all I had to say about decimal numbers aka decimals in this “something about” section. I believe there could be much more to say, but I can’t think of anything essential right now.

So, best of luck, and thank you (and me) for your (mine) time. :-)

p.s. Ah, yes. I cooking up some dividing decimals so this isn't over...

Go from Multiplying and dividing decimals to Help with decimals

Go from Multiplying and dividing decimals to Free Math Help Online - Home Page