Adding Fractions With Unlike Denominators - Solving Fraction problems

Adding Fractions
With Unlike Denominators

The whole wisdom about this adding fractions business is in "equalizing" the denominators, and the only way to do that is by expanding or simplifying fractions. After that addition boils down to simple adding of numerators.

We’re going to start as simple as we can, and then build our way up to more complex examples.

On the previous page, we've already covered the following:

Adding fractions with like denominators:

And now it's time to cover:

Adding fractions with unlike denominators:

numerator = 1, unlike denominators
numerator > 1, unlike denominators

But before we start here's something you should:

REMEMBER:
In pizza language - We can’t count different pizza slice sizes, (i.e. denominators).
First we must take our pizza knife and cut to make all pizza slices alike (i.e. find a LCD - least common denominator), only then we can count the slices (add fractions). :-)

So first, let's look at our

First case of
Adding Fractions with Unlike Denominators

Numerators = 1
Different Denominators

This is a really simple example with different denominators - adding 1/2 adn 1/3.

Halves and thirds are like "apples" and "oranges", we can’t quantify two different sizes, so we have to make them the same.


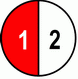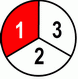
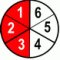
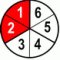
1	×3	+	1	×2	=	3	+	2	=	5
2	×3	+	3	×2	=	6	+	6	=	6

We’re "complicating" (expanding) our fractions by multiplying both numerator and denominator with a same number to get the equivalent pair for our same-denominators sum, i.e. LCD.

After that "transformation" our case becomes simple. We add the numerators, see if we’ve crossed over to some whole numbers (in this particular case we didn’t 5/6<1), and that’s it. There was nothing to reduce so we move on to the next combination.

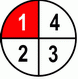
In the following example we see that we don’t need to expand our second fraction, because 4 is already a LCD for 2 and 4.


1	×2	+	1	=	2	+	1	=	3
2	×2	+	4	=	4	+	4	=	4

Boring reminder: We don’t add the denominators, just numerators.

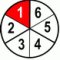
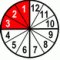
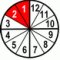
Before we move to examples with numerator greater than 1, let's see one more addition - adding 1/4 and 1/6.


1	×3	+	1	×2	=	3	+	2	=	5
4	×3	+	6	×2	=	12	+	12	=	12

Now let’s put some numerators into game.

Second case of
Adding Fractions with Unlike Denominators

Numerators > 1
Different Denominators


3	×3	+	2	×4	=	9	+	8	=	17	=	1	5
4	×3	+	3	×4	=	12	+	12	=	12	=	1	12

Even with numerators being greater than 1, our addition with unlike denominators hasn’t complicated much. After we find our LCD, in this case 12, we end up with plain addition of numerators.

Here's another example:


5	+	4	×2	=	5	+	8	=	13	=	2	1
6	+	3	×2	=	6	+	6	=	6	=	2	6

Now some thirds and fourths.


5	×4	+	5	×3	=	20	+	15	=	35	=	2	11
3	×4	+	4	×3	=	12	+	12	=	12	=	2	12

That's the principle. Analogy goes for any other fraction addition. Now all you need is some worksheets to practice (hopefully coming soon).

Anyway, let's summerize below.

Conclusion
for adding fractions with unlike denominators page:

You can't add any fractions until you make their denominators alike (by finding a Least Common Denominator)
Once there - add the numerators
Finally reduce if necessary, and write it in desired fraction form (unproper or mixed)

If you want to go back to adding fractions with like denominators page.